发表于 | 分类于 | 0 | 阅读次数 1146

前言

一直以来对图形学都颇为想系统的入门，平时零零碎碎的学习到零星半点，刚好发现这个课程，讲的甚好，颇为符合我的接受范围，以此记录自己的学习记录。

如有纰漏，望加指正

课程信息

视频链接：https://www.bilibili.com/video/av90798049
课程资源：https://sites.cs.ucsb.edu/~lingqi/teaching/games101.html
导师论文：https://sites.cs.ucsb.edu/~lingqi/publications/thesis_final.pdf
讨论网站： https://games-cn.org/

P1 Overview of Computer Graphics（计算机图形概述）

课件：https://sites.cs.ucsb.edu/~lingqi/teaching/resources/GAMES101_Lecture_01.pdf
作业：无

  • 什么是计算机图形（学）？
  • 为什么学习计算机图形（学）？
  • 课程主题
  • 课程储备

书籍推荐： Fundamentals of Computer Graphics

P2 Review of Linear Algebra （线性代数回顾）

课件：https://sites.cs.ucsb.edu/~lingqi/teaching/resources/GAMES101_Lecture_02.pdf
作业：作业0

图形学依赖

  • 基础数学
    • 线性代数、微积分、统计
  • 基础物理
    • 光学、力学
  • 其他
    • 信号处理
    • 数值分析
  • 和一些美学

课件大概

  • 向量
    • 向量归一化
    • 向量加法
    • 笛卡尔坐标
    • 向量乘法
      • 点积
      • 叉积
      • 正交基和坐标系
  • 矩阵（代表变换）
    • 平移、旋转、裁剪、缩放
    • 矩阵与矩阵的乘法
    • 矩阵与向量的乘法
    • 矩阵的转置
    • 逆矩阵
    • 向量矩阵形式的乘法

主要讲了

  • 向量的表示、性质、计算以及向量的点积和叉积的应用
  • 矩阵的性质、计算以及应用

完成作业0

  1. 如何用VBox创建64bit的系统？
    要在Bios界面打开CPU的VT（Visutal Techology)
  2. 设置正确的分辨率1920*1080
  3. 安装好增强工具
  4. 使用VSCode跑示例Cpp （了解VSCode常用快捷键 https://zhuanlan.zhihu.com/p/44044896 ）
  5. 了解Eigen库的使用，按照作业引导做一遍
  6. 创建一个新的hw0 folder 在其中创建hw0.cpp
  1. 使用Cmake进行build
3.2 编译
为方便之后的作业编写，本次作业要求使用 cmake 进行编译。
首先，编写好本次作业的程序 main.cpp。
然后, 在 main.cpp 所在目录下，打开终端 (命令行)，依次输入：
• mkdir build: 创建名为 build 的文件夹。
• cd build: 移动到 build 文件夹下。
• cmake ..: 注意其中’..’ 表示上一级目录，若为’.’ 则表示当前目录。
• make: 编译程序，错误提示会显示在终端中。
• ./Transformation：若上一步无错误，则可运行程序 (这里的 Transformation
为可执行文件名，可参照 CMakeLists.txt 中修改)。
  1. 运行无误，提交

P3 Transformation （变换）

课件：https://sites.cs.ucsb.edu/~lingqi/teaching/resources/GAMES101_Lecture_03.pdf
作业：

Dot Product

  • Forward / backward (dot product positive / negative)

Cross Product

  • Left / right (cross product outward / inward)

今天讲

  • 为什么学习变换
  • 2D变换：旋转、缩放、剪切
  • 齐次坐标
  • 组合变换
  • 3D变换

..

  1. 用矩阵表示变换

  2. 仿射变换与齐次坐标

    • 2D
      点：(x,y,1)
      向量(x,y,0)
    • 3D
      点：（x,y,z,1)
      向量：（x,y,z,0）

2DTransform.jpg

  1. 组合变换（注意变换顺序）

P4 Transformation Cout. (变换续)

课件：https://sites.cs.ucsb.edu/~lingqi/teaching/resources/GAMES101_Lecture_04.pdf
作业：

重点：

Viewing transformation 观测变换

  • View(视图)/Camera transformation
  • Projection(投影） transformation
    • Orthographic(正交） projection
    • Perspective(透视）projection

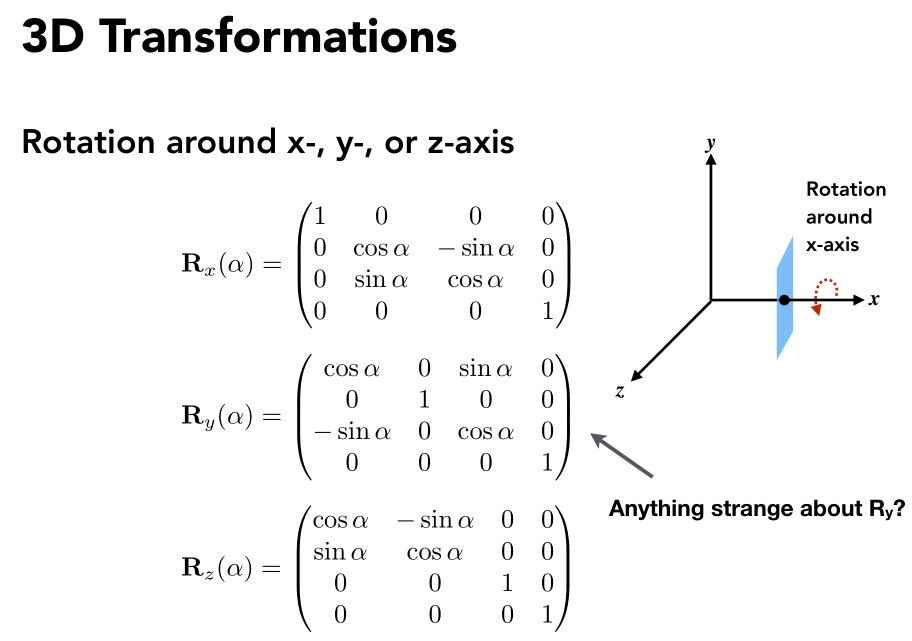
3D Transform
3DTransform01.jpg

3DTransform02.jpg

想象如何拍照

  • 找到一个好的位置放置人（model transformation）模型变换
  • 找到一个好的角度放相机 （view transformation) 视图（相机）变换
  • 拍照！ （projection transformation） 投影变换
    也就是常说的MVP

什么是视图（相机）变换

如何进行视图变换

  • 定义相机
    • 相机的位置 Position
    • 相机观察方向 Look-at direction
    • 相机垂直方向 Up Direction

P5 光栅化1

在屏幕空间采样

抗锯齿

Homework 1

P6 光栅化2

信号处理

  1. Last Lectures
  • Viewing
    • View + Projection + Viewport
  • Rasterizing triangles
    • Point-in-triangle test
    • Aliasing
  1. Today
  • Antiliasing（反走样）（抗锯齿）
    • Sampling theory
    • Antialiasing in practice
  • Visiblity/occlusion
    • Z-buffering

Aliasing(走样) 锯齿？ 如何抗锯齿

采样

Sampling Artifacts 采样瑕疵
(Erros/Mistakes/Inaccuracies) in Computer Graphics

  • jaggies （锯齿） sampling in space
  • Moire Patterns in Imaging (摩尔纹) undersampling images
  • Wagon wheel effect sampling in time
  • Many more

Antialiasing Idea 反走样方法
先对信号模糊（滤波），再采样

Frequency Domain 频域
频率、周期

傅里叶变化
傅里叶级数展开
所有的信号，都可以通过正弦和余弦信号叠加成。

更高的频率需要更快的采样

走样的概念

Filtering = Getting rig of certain frequency contents (滤波)

High-pass filter 高通滤波
Low-pass filter 低通滤波 （Blur）

Filter Out Low and High Frequencies

Filtering = Convolution(卷积) ( = Averaging)

Convolution Theorem(卷积定理)
时域的卷积 = 频域的乘积

Box Filter

Sampling = Repeating Frequency Contents

原始函数
冲击函数
采样结果

Aliasing = Mixed Frquency Contents

AntiAliaing
How Can We Reduce Aliasing Error?

  1. Increase sampling rate
  2. Antialiasing
    Antaialiasing By Supersampling(MSAA)
    先做一个模糊（低通滤波），砍掉高频。 再采样

MSAA的消耗

抗锯齿：

  • FXAA （Fast Approximate AA） 有点像后期处理边界。
  • TAA (Temporal AA)

Super resolution/ Super sampling (超分辨率，超采样)

  • From low resolution to high resolution
  • Essentially still "not enough samples" problem
  • DLSS(Deep Learning Super Sampling)

P7 光照、着色和图形管线

Homework2 放出来
About Z-Buffering

Last Lectures
Rasterization

  • Rasterizing one triangle
  • Sampling theory
  • Antialiasing

Today

  • Visibility/occlusion
    • Z-buffering
  • Shading
    • Illumination & Shading
    • Graphics Pipeline

Painter's Algorithm (画家算法)
inspired by how painters paint
Paint from back to front, overwrite in the framebuffer

Z-Buffer
This is the algorithm that eventually won.
Idea:
- Store current min. z-value for each sample(pixel)
- Needs an addtional buffer for depth values
- frame buffer stores color values
- depth buffer(z-buffer) stores depth

IMPORTANT: For simplicity we suppose z is always positive

Initialize depth buffer to 无限大
···

Z-buffer Complexity
Complexity

  • O(n) for n triangles(assuming constant coverage)
  • How is it possible to sort n triangles in linear time?

Drawing triangles in different orders?

Most important visibility algorithm

  • Implemented in hardware for all GPUs （几乎所有GPU都支持）

透明物体？？ 需要特殊处理

Shading
定义

在本课程中， 对不同的物体应用不同的材质

A Simple Shading Model
( Blinn-Phong Reflectance model)